A two sample t-test allows us to determine whether there is a statistically significant difference in means between two independent groups (or populations). The two groups are identified by a categorical predictor variable (i.e. a categorical predictor with two levels). The response variable is quantitative (and most often, continuous).
For this type of t-test, the two groups must be independent of each other. That means that responses from individuals in one group do not affect responses from individuals in the other group. This is usually accomplished by making sure the two groups do not overlap (no shared individuals) and that there is no relationship between individuals across the groups. For instance, it would be more appropriate to use another kind of t-test (a paired t-test) if you were interested in comparing the heart rate of the same individuals before and after exercise. These observations are paired between each individual has two measurements, so there is a specific one-to-one relationship between individuals in the observed groups. However, if you were interested in heart rates of athletes versus non-athletes, you would use a two-sample test. One group is the athletes and the other is the non-athletes, and we would not expect relationships between heart rates between the two groups unless there was some other sort of pairing going on.
Example
Professor Temeles studies plant pollinator interactions. Sometimes bees ‘rob’ flowers of their nectar by piercing the flower from the outside to obtain nectar rather than by entering the flower and picking up pollen which then gets transferred to other plants. This means that the plant does not obtain the benefit of pollination, but the bee does obtain nectar. Pierced flowers may suffer other consequences, with one potentially being a shorter life span (hours) of the flower.
Thus, we are interested in whether there is a difference in average life span of flowers pierced by bees as opposed to those not pierced by bees. In this case, we will have a directional hypothesis in that, we expect the unpierced flowers to live longer.
HO: Mean life span of unpierced flowers is not longer than pierced flowers.
HA: Mean life span of unpierced flowers is longer than pierced flowers.
If there we did not have an idea of which would live longer, we could still test for differences, but instead would have a null hypothesis indicating that there should be no difference in life span by group and an alternative that there is a difference in life span by group. In the case that you have a directed alternative hypothesis, that is called a one-sided test, and it will be associated with a one-tailed P-value. When there is no direction (i.e. you are just looking to see if there is a difference and do not specify which group’s mean will be higher), that is called a two-sided test, and will be associated with a two-tailed P-value.
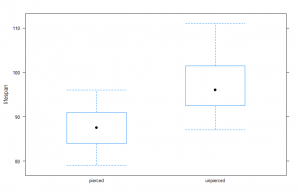
Not all tests have one-sided and two-sided options, but t-tests do. When running a one-sided test, it makes sense to look at your data and see if the observed values at least seem to support the alternative, otherwise, it’s not reasonable to run the test. For example, in our data, the observed mean lifespan for unpierced flowers was 97.4 and the mean lifespan for pieced flowers was 87.5. It looks like our alternative hypothesis is reasonable – the unpierced mean is larger than the pierced mean, and we run the test to see if the difference is statistically significant. If we had suggested the mean for pierced flowers was supposed to be larger than for unpierced flowers, we wouldn’t run the test. Our data wouldn’t support that hypothesis.