Standard error is a related form of variation to standard deviation. Standard error is often reported in scientific articles. To understand standard error, we need to chat a little bit about looking at variation in statistics, not just variation in variables in your data set.
Let us suppose we are considering the fiddler crab example, with n=11 female fiddler crabs having their largest claw measured. These are 11 female fiddler crabs out of thousands that could have been selected. So, we take our sample of 11 and record their measurements, and then save the (arithmetic/sample) mean of those measurements. Now imagine each lab takes a sample of n=11 female fiddler crabs from the population of fiddler crabs. Everyone will compute their own sample mean. Would you expect everyone to get the same sample mean you have?
No. I might get a mean of 7.3 (as above), and yours might be 7.4, or 8.2, or 6.9. Would you want the sample means to be very different from each other?
No. All the sample means are trying to estimate the same quantity – the population mean. The idea is, we want to be able to talk about the variability (variation or spread) in the sample means! This is different than the variability we talked about above, which is variation IN a sample. Here, the idea is to understand variation in a statistic – because we understand that statistics will vary from sample to sample.
Now, statisticians have done the hard work here. You can determine, under certain conditions, what the behavior of some common statistics are, including the behavior of the sample mean. (If you take an introductory statistics course, look for the discussion about sampling distributions or the Central Limit Theorem).
In short, statisticians can actually give you a formula for the standard deviation of the sample mean when appropriate conditions are met. The issue is that formula involves the population standard deviation (sigma) which is usually unknown. But we still want an estimate of the variability in the sample means! So what can we do?
We compute the standard error instead of the standard deviation for the sample mean. If we cannot compute the standard deviation of the sample mean because we do not know the population standard deviation, we estimate the population standard deviation with the sample standard deviation. That gives us the standard error of the sample mean.
In summary, statistics vary from sample to sample, and we can describe the variability in our statistics (under certain conditions), but may have to estimate it. The standard error of the sample mean allows us to estimate the standard deviation of the sample mean, so that we can understand the spread of sample means.
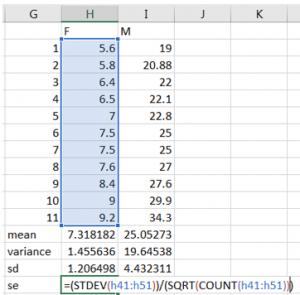
To calculate the standard error of a sample mean, we divide the sample standard deviation by the square root of the sample size. Again, this formula comes from a theoretical result – but don’t worry about that part! Other standard errors for other statistics exist, but this one is fairly commonly used – it is useful anytime you are working with the sample mean.
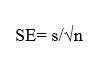
Excel
=(STDEV.S(cell:cell))/(SQRT(COUNT(cell:cell)))